Table of contents


Given problem

Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become:

  • [4,5,6,7,0,1,2] if it was rotated 4 times.
  • [0,1,2,4,5,6,7] if it was rotated 7 times.

Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]].

Given the sorted rotated array nums of unique elements, return the minimum element of this array.

You must write an algorithm that runs in O(log n) time.

Example 1:

Input: nums = [3,4,5,1,2] Output: 1 Explanation: The original array was [1,2,3,4,5] rotated 3 times. Example 2:

Input: nums = [4,5,6,7,0,1,2] Output: 0 Explanation: The original array was [0,1,2,4,5,6,7] and it was rotated 4 times. Example 3:

Input: nums = [11,13,15,17] Output: 11 Explanation: The original array was [11,13,15,17] and it was rotated 4 times.

Constraints:

  • n == nums.length
  • 1 <= n <= 5000
  • -5000 <= nums[i] <= 5000
  • All the integers of nums are unique.
  • nums is sorted and rotated between 1 and n times.


Some properties of a rotated array

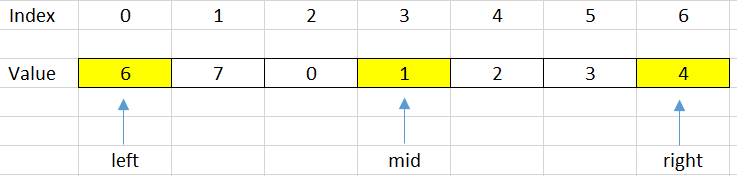
  • When we divide a rotated array into two halves, at least one of the two halves will always sorted.

    To understand this property, we can see a below image:

    If we choose the mid = 3 as the pivot point, we can find that our array is divided into two halves that are increased arrays.

    –> So we can apply Binary Search for problems that are relevant to rotated array.


Solutions for this problem

To solve this problem, we can have two solutions:

  • Linear Search

    The simple solution to solve it is to use Linear Search. We can scan all elements and compare them with the minimum element.

  • Binary Search

    Because the a part of array is sorted, so we can use Binary Search to solve it.


Below is our source code about this way.

public static int findMinElement(int[] arr) {
    int minPos = 0;
    for (int i = 1; i < arr.length - 1; ++i) {
        if (arr[minPos] > arr[i]) {
            minPos = i;
        }
    }

    return minPos;
}

The complexity of Linear Search:

  • Time complexity: O(n) - n is the number of elements of this array
  • Space complexity: O(1)


Using Binary Search algorithm

  1. Using Template #1

    In a rotated array, we will have some cases that we will cope with when shift it.

    • Case 1 - when sorted array is not rotated with any steps

      In this case, our array is a sorted array but does not rotate with any steps. So, to check this case, we do the below expression:

        if (arr[left] <= arr[high]) {
      return left;
  }

    • Case 2 - When our mid index points to the minimum element

      So, we will check it by using the following condition:

        int next = (mid + 1) % n;   // n is the length of the array
  int prev = (mid + n - 1) % n;

  if (arr[mid] < arr[next] && arr[mid] < arr[prev]) {
      return mid;
  }

    • Case 3 - When our mid index points to the element that is belong to the sub-array. It does not contains the minimum element.

      In order to know exactly how we are under this case, we will use the below condition:

        if (arr[left] <= arr[mid]) {
      left = mid + 1;
  }

      Due to the minimum element that is belong to the other side, so we will shift the right side.

    • Case 4 - When our mid index points to the element that is belong to the sub-array. It contains the minimum element.

        if (arr[mid] <= arr[right]) {
      right = mid - 1;
  }

    Based on the four conditions, we will have source code for this problem:

     class Solution {
     public int findMin(int[] arr) {
         int len = arr.length;
         int left = 0;
         int right = len - 1;

         while (left <= right) {
             if (arr[left] <= arr[right]) {  // Case 1: sorted array
                 return arr[left];
             }

             int mid = left + (right - left) / 2;
             int next = (mid + 1) % len;
             int prev = (mid + len - 1) % len;
             if (arr[mid] <= arr[next] && arr[mid] <= arr[prev]) {   // Case 2: mid index points to the minimum element
                 return arr[mid];
             } else if (arr[mid] <= arr[right]) {    // Case 4
                 right = mid - 1;
             } else if (arr[mid] >= arr[left]) {     // Case 3
                 left = mid + 1;
             }
         }

         return -1;
     }
 }

  2. Using Template #2

     class Solution {
     public int findMin(int[] nums) {
         if (nums == null) {
             return -1;
         }

         int left = 0;
         int right = nums.length - 1;

         while (left < right) {
             int mid = left + (right - left) / 2;

             if (nums[mid] > nums[right]) {
                 left = mid + 1;
             } else {
                 right = mid;
             }
         }

         return nums[left];
     }
 }

  3. Using Template #3

    • Comparing between mid and right position.

      Due to the comparison between mid and right, the initial value of right will be the index of the last element in an array.

        int right = nums.length - 1;

      The property of a rotated array is that it divides our array into two sorted array in ascending order. So we can choose different points to move mid. In this case, we will choose right position. In the next way, we will choose left position.

      Below is some cases that we take care:

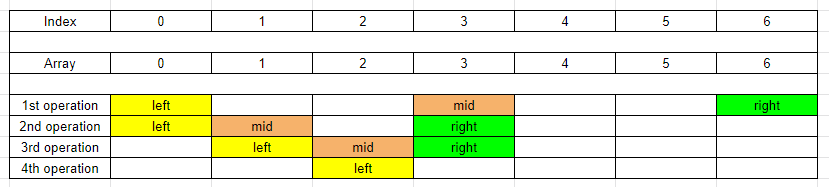
      • 1st case - No rotation or the number of rotations is equal to the length of the array.

      • 2nd case - The mid points to the minimum element in the array.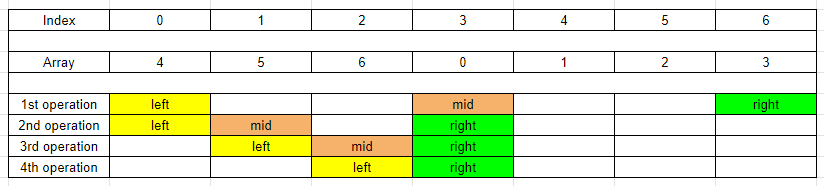

        We can easily find that it’s the same with the above one.

      • 3rd case - The mid points to the second child sorted array.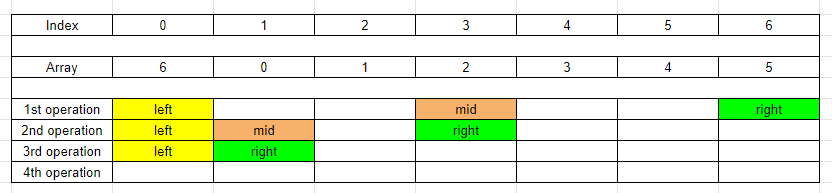

      • 4th case - The mid points to the first child sorted array.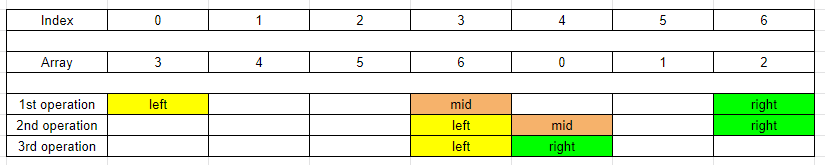

      Below is our source code.

        class Solution {
      public int findMin(int[] nums) {
          int low = 0;
          int high = nums.length - 1;

          while (low + 1 < high) {
              int mid = low + (high - low) / 2;

              if (nums[mid] > nums[high]) {
                  low = mid;
              } else {
                  high = mid;
              }
          }

          return nums[low] < nums[high] ? nums[low] : nums[high];
      }
  }

    • Comparing between mid and left position.

        public class Solution {
      public int findMin(int[] nums) {
          int pivot = this.findPivot(nums);
          return Math.min(nums[0], nums[pivot]);
      }

      private int findPivot(int[] nums) {
          int left = 0;
          int right = nums.length;

          while (left + 1 < right) {
              int mid = left + (right - left) / 2;

              if (nums[mid - 1] > nums[mid]) {
                  return mid;
              } else if (nums[left] < nums[mid]) {
                  left = mid;
              } else {
                  right = mid;
              }
          }

          return left;
      }
  }

The complexity of this solution:

  • Time complexity: O(logn)
  • Space complexity: O(1)


Wrapping up

  • Understanding how to use some templates of Binary Search algorithm.

  • Understanding about what the rotated array is, and its properties.

  • When we have two different trends in our array, we can use Binary Search to solve this problem.

  • From this problem, we can find that in a rotated array, the index of the minimum element will be equal to the number of rotation of its array.

  • Learn how to get the index of the next element in the rotated array by using modulo of the length of the array.


Refer:

153. Find Minimum in Rotated Sorted Array