Table of contents

• Given problem
• How selection sort works
• Source code
• When to use
• Wrapping up

Given problem

Suppose we have an array, we need to sort this array followed by increasing order.

In this article, we will use selection sort to deal with this problem.

How selection sort works

The idea of the selection sort is that:

• at the step ith, we need to choose the mimimum element in the array a[i], ..., a[n - 1].

• Then, iterate all element from i + 1 to n - 1, compare a[i] and a[j] with j = i + 1, ..., n, and save the index of the minimum element in the minIndex variable.

• At the end of ith loop, we will exchange value between a[i] and a[minIndex].

• Finally, we will have a sorted array.

Belows are some steps to describe the implementation of selection sort.

1. Original array

   

2. At 0th position, select a[0] as the minimum element of the array has range from 0 to n - 1.

   • Iterate all elements from 1 to n - 1.

   • Find the index = 6 is the minimum element.

   • Swap a[0] and a[6].

   

3. At 1st position, select a[1] as the minimum element of the array has range from 1 to n - 1.

   • Iterate all elements from 2 to n - 1.

   • Find the index = 2 is the minimum element.

   • Swap a[1] and a[2].

   

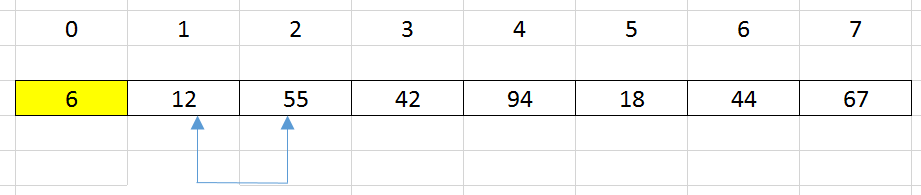
   Then, we have our array looks like that:

   

4. At 2nd position, select a[2] as the minimum element of the array has range from 2 to n - 1.

   • Iterate all elements from 3 to n - 1.

   • Find the index = 5 is the minimum element.

   • Swap a[2] and a[5].

   

   Then, we have our array looks like that:

   

5. At 3rd position, select a[3] as the minimum element of the array has range from 3 to n - 1.

   • Iterate all elements from 4 to n - 1.

   • Find it is the minimum element, so we do not need to swap anything.

   Then, we have our array looks like that:

   

6. At 4st position, select a[4] as the minimum element of the array has range from 4 to n - 1.

   • Iterate all elements from 5 to n - 1.

   • Find the index = 6 is the minimum element.

   • Swap a[4] and a[6].

   

   Then, we have our array looks like that:

   

7. Continue to do that, we have our final array.

   

Source code

public static void selectionSort(int[] nums) {
    int length = nums.length;

    for (int i = 0; i < length; ++i) {
        int minIndex = i;

        for (int j = i + 1; j < length; ++j) {
            if (nums[j] < nums[minIndex]) {
                minIndex = j;
            }
        }

        // swap value at the minIndex and i
        int tmp = nums[minIndex];
        nums[minIndex] = nums[i];
        nums[i] = tmp;
    }
}

The complexity of the selection sort:

• Time complexity: O(n^2)
• Space complexity: O(1)

Selection sort is not stable sorting algorithm.

When to use

• When our array has the small size.

• When our array is not partially sorted.

Wrapping up

• Understanding the idea of the selection sort, and how to implement it.