Table of contents

• Given problem
• How insertion sort works
• Source code
• When to use
• Wrapping-up

Given problem

Suppose we have an array, we need to sort this array followed by increasing order.

In this article, we will use insertion sort to deal with this problem.

How insertion sort works

The idea of insertion sort is that assuming that based on an sorted array a[0], ..., a[i - 1], we want to determine a suitable position of a[i] element to insert it into this array.

Normally, we will go backward from i - 1 index to 0 index. If a[i] < a[i - 1], swap them.

Belows are some steps to use insertion sort with the above array.

1. Original array

   

2. Insert a new element at the index = 1 into the array’s length = 1, from index = 0.

   

   We can find that a new element with value = 55 is always greater than 44. So, we do not swap them.

   Then, our new array that contains both 44, 55 is sorted.

   

3. Insert a new element at the index = 2 into the array’s length = 2, from index = 0.

   

   A new element has value = 12 that is less than other elements in our new array.

   Applying the idea of insertion sort, go backward from index = 2 to index = 0, compare a couple element, then swap them.

   

   

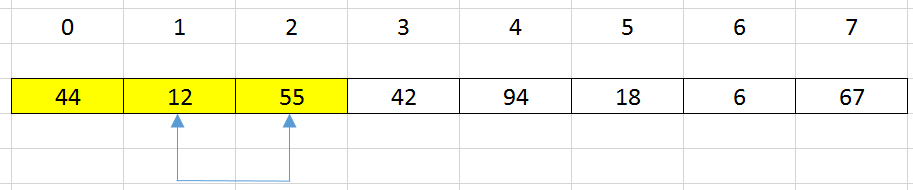
   Now, we have our new sorted array:

   

4. Insert a new element at the index = 3 into the array’s length = 3, from index = 0.

   

   

   

   Then, we have a sorted array:

   

5. Continue to the other elements, we have the original sorted array.

   

Source code

Belows are some versions of the insertion sort’s implementation.

1. Version 1

    public static void insertionSort(int[] nums) {
        int length = nums.length;
   
        for (int i = 1; i < length; ++i) {
            for (int j = i; j > 0; --j) {
                if (nums[j] < nums[j - 1]) {
                    // exchange value between nums[j] and nums[j - 1]
                    int tmp = nums[j];
                    nums[j] = nums[j - 1];
                    nums[j - 1] = tmp;
                }
            }
        }
    }
   
   

2. Version 2

    public static void insertionSortVersion2(int[] nums) {
        int length = nums.length;
   
        for (int i = 1; i < length; ++i) {
            int key = nums[i];
            int j = i - 1;
   
            // shift elements to right side if key < nums[j]
            while (j >= 0 && key < nums[j]) {
                nums[j + 1] = nums[j];
                --j;
            }
   
            nums[j + 1] = key;
        }
    }
   
   

The complexity of the insertion sort is:

• Time complexity:

  • Worst case: O(n^2) with an array in the descending order.

• Space complexity: O(1)

Insertion sort is a stable sorting algorithm because the order of equal elements is maintained after sorted.

When to use

• When our array is nearly sorted.

• When our array has the small size.

• When we need to sort elements online - that is sorting them as they come in.

  Because the idea of insertion sort is that suppose we have an sorted array, then insert a new element into it. Our new array is still sorted.

Wrapping up

• Understanding about some versions of insertion sort: exchange and shift elements.

Refer:

https://www.acodersjourney.com/insertion-sort/