Table of contents
Given problem
There are n friends that are playing a game. The friends are sitting in a circle and are numbered from 1 to n in clockwise order. More formally, moving clockwise from the ith friend brings you to the (i+1)th friend for 1 <= i < n, and moving clockwise from the nth friend brings you to the 1st friend.
The rules of the game are as follows:
- Start at the
1stfriend. - Count the next
kfriends in the clockwise direction including the friend you started at. The counting wraps around the circle and may count some friends more than once. - The last friend you counted leaves the circle and loses the game.
- If there is still more than one friend in the circle, go back to step
2starting from the friendimmediately clockwiseof the friend who just lost and repeat. - Else, the last friend in the circle wins the game.
Given the number of friends, n, and an integer k, return the winner of the game.
Example 1:
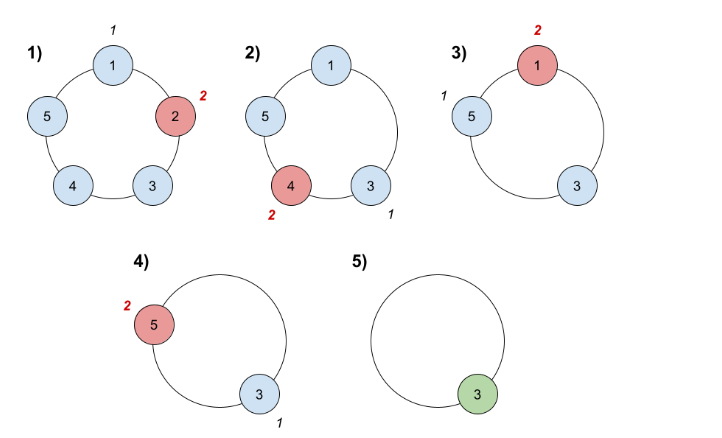
Input: n = 5, k = 2
Output: 3
Explanation: Here are the steps of the game:
1) Start at friend 1.
2) Count 2 friends clockwise, which are friends 1 and 2.
3) Friend 2 leaves the circle. Next start is friend 3.
4) Count 2 friends clockwise, which are friends 3 and 4.
5) Friend 4 leaves the circle. Next start is friend 5.
6) Count 2 friends clockwise, which are friends 5 and 1.
7) Friend 1 leaves the circle. Next start is friend 3.
8) Count 2 friends clockwise, which are friends 3 and 5.
9) Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.
Example 2:
Input: n = 6, k = 5
Output: 1
Explanation: The friends leave in this order: 5, 4, 6, 2, 3. The winner is friend 1.
Constraints:
- 1 <= k <= n <= 500
Using Circular Linked List
The first approach is to use brute force algorithm. It means that we will create a circular linked list to simulate all steps above.
Below is the source code of this way.
class Solution {
public int findTheWinner(int n, int k) {
CircularLinkedList circularGame = new CircularLinkedList();
for (int i = 1; i <= n; ++i) {
circularGame.insert(i);
}
int count = k;
CircularLinkedList.Node currentNode = circularGame.head();
while (circularGame.hasNotRemainedOne()) {
CircularLinkedList.Node kNode = circularGame.incrementWithSteps(currentNode, count);
currentNode = kNode.next;
circularGame.remove(kNode);
}
return circularGame.head().value;
}
class CircularLinkedList {
private Node head;
private Node tail;
public void insert(int value) {
Node newNode = new Node(value);
if (this.head == null) {
head = newNode;
} else {
this.tail.next = newNode;
}
this.tail = newNode;
this.tail.next = head;
}
public void remove(Node node) {
if (node == null) {
return;
}
Node currentNode = this.head;
do {
if (currentNode.next == node) {
currentNode.next = node.next;
if (this.head == node) {
this.head = this.head.next;
}
if (this.tail == node) {
this.tail = currentNode;
}
break;
}
currentNode = currentNode.next;
} while (currentNode != this.head);
}
public boolean hasNotRemainedOne() {
return this.head != this.tail;
}
public Node incrementWithSteps(Node startNode, int k) {
if (k == 1) {
return startNode;
}
if (k < 1 || startNode == null) {
return null;
}
Node currentNode = startNode;
do {
currentNode = currentNode.next;
--k;
} while (k != 1);
return currentNode;
}
public Node head() {
return this.head;
}
static class Node {
public Node next;
public int value;
public Node(int value) {
this.value = value;
this.next = null;
}
}
}
}
The complexity of this solution:
- Time complexity: O(n)
- Space complexity: O(n)
Using Queue
To reduce the number of line of code in the above solution, we can use Queue data structure. The logic is still remained.
class Solution {
public int findTheWinner(int n, int k) {
Queue<Integer> circularGame = new LinkedList<>();
for (int i = 1; i <= n; ++i) {
circularGame.add(i);
}
while (circularGame.size() > 1) {
int count = k;
while (count > 1) {
int current = circularGame.poll();
circularGame.add(current);
--count;
}
circularGame.poll();
}
return circularGame.peek();
}
}
Wrapping up
-
When running the two solutions in the leetcode, we found that:
- The way that use CircularLinkedList is running faster than Using Queue data structure, because using Queue took 125 ms, but Using Circular Linked List took 8 ms.
Reference: