Table of contents

• Given problem
• Using Linear Search to find element
• Using Binary Search
• Wrapping up

Given problem

There is an integer array nums sorted in ascending order (with distinct values).

Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed).

For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].

Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.

You must write an algorithm with O(log n) runtime complexity.

Example 1:

• Input: nums = [4,5,6,7,0,1,2], target = 0
• Output: 4

Example 2:

• Input: nums = [4,5,6,7,0,1,2], target = 3
• Output: -1

Example 3:

• Input: nums = [1], target = 0
• Output: -1

Constraints:

• 1 <= nums.length <= 5000
• -104 <= nums[i] <= 104
• All values of nums are unique.
• nums is an ascending array that is possibly rotated.
• -104 <= target <= 104

Using Linear Search to find element

Normally, the first thing we do is to use brute-force to deal with problem. In this case, we will use linear search to do it.

public static int search(int[] nums, int target) {
    int pos = 0;
    for (int i = 0; i < nums.length - 1; ++i) {
        if (nums[i] == target) {
            pos = i;
            break;
        }
    }

    return pos;
}

The complexity of using Linear Search is:

• Time complexity: O(n)
• Space complexity: O(1)

Using Binary Search

The drawback of using Linear Search is about the time complexity - O(n). But we can improve it in O(logn), because our rotated array has sub-arrays that are increased array.

So we can use Binary Search.

• First way.

  Next, we will analyze our problem when using Binary Search’s the first invariant.

  1. Case 1 - When we jump into the right sub-array

     

     But in this case, we can have two issues:

     • our target will under this range.

       For example: target = 2, then we have:

       

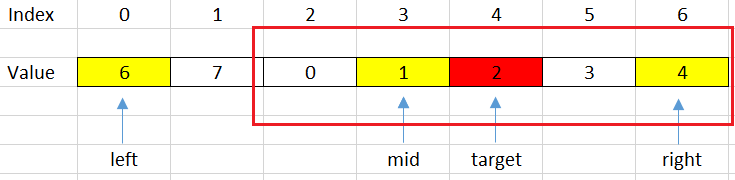
       Then, we will shift left with steps: left = mid + 1;

     • our target will not be contain in this range.

       For example: target = 7, then we have:

       

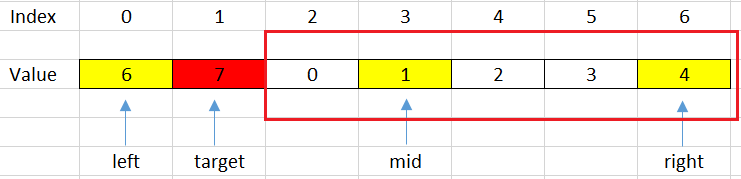
       Then, we will shift right with steps: right = mid - 1;

     Based on the above conditions, we can have the segment code:

      if (nums[mid] <= nums[right]) {
          if (nums[mid] < target && target <= nums[right]) {
              left = mid + 1;
          } else {
              right = mid - 1;
          }
      }
     

  2. Case 2 - When we jump into the left sub-array

     

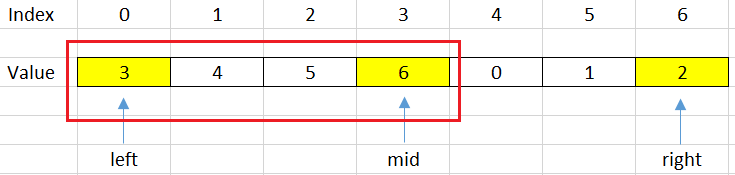
     But in this case, we also have two issues:

     • our target will under this range.

       For example: target = 4, it can be described in a below image.

       

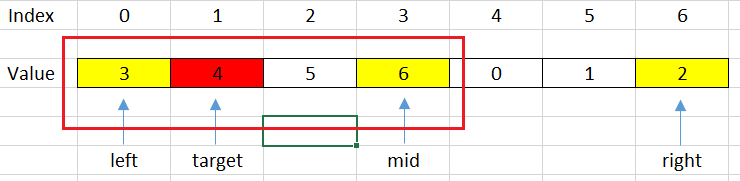
       Then, we will shift left with some steps: right = mid - 1;

     • our target will be not contain in this range.

       For example, target = 1, then we have:

       

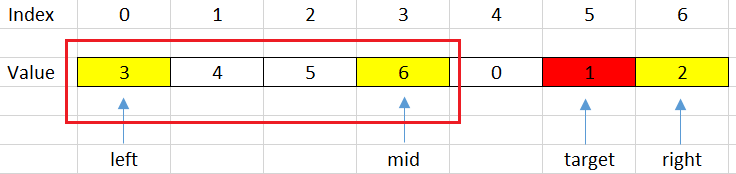
       Then, we will shift right with some steps: left = mid + 1;

     Based on above conditions, we can some code to describe it.

      if (nums[mid] >= nums[left]) {
          if (nums[left] < target && target < nums[mid]) {
              right = mid - 1;
          } else {
              left = mid + 1;
          }
      }
     

  Below is our source code of this way:

  • First invariant of Binary Search.

      public static int search(int[] nums, int target) {
          int left = 0;
          int right = nums.length - 1;
    
          while (left <= right) {
              int mid = left + (right - left) / 2;
              if (nums[mid] == target) {
                  return mid;
              }
    
              if (nums[mid] <= nums[right]) { // right half is sorted
                  if (target > nums[mid] && target <= nums[right]) {
                      left = mid + 1;
                  } else {
                      right = mid - 1;
                  }
              } else {        // left half is sorted
                  if (nums[left] <= target && target < nums[mid]) {
                      right = mid - 1;
                  } else {
                      left = mid + 1;
                  }
              }
          }
    
          return -1;
      }
    

  • Third invariant of Binary Search.

      class Solution {
          public int search(int[] nums, int target) {
              int left = 0;
    
              // The initially condition of right variable is not correct when using the template of Binary Search's third invariant.
              // But in this problem, we need to use it to pass all test case in LeetCode.
              int right = nums.length - 1;
    
              while (left + 1 < right) {
                  int mid = left + (right - left) / 2;
    
                  if (nums[mid] == target) {
                      return mid;
                  } else if (nums[mid] > nums[left]) {    // 1st sorted sub-array
                      if (nums[left] <= target && target <= nums[mid]) {
                          right = mid;
                      } else {
                          left = mid;
                      }
                  } else {    // 2nd sorted sub-array
                      if (right < nums.length && nums[mid] <= target && target <= nums[right]) {
                          left = mid;
                      } else {
                          right = mid;
                      }
                  }
              }
    
              if (nums[left] == target) {
                  return left;
              }
    
              if (right < nums.length && nums[right] == target) {
                  return right;
              }
    
              return -1;
          }
      }
    

• Second way.

  We can search pivot point in this sorted rotated array. Then, search the target on each sub-array.

    class Solution {
        public int search(int[] nums, int target) {
            int pivot = findPivot(nums);
  
            int res = binarySearch(nums, 0, pivot, target);
            if (res != -1) {
                return res;
            }
  
            return binarySearch(nums, pivot, nums.length, target);
        }
  
        private int findPivot(int[] nums) {
            int left = 0;
            int right = nums.length;
  
            while (left + 1 < right) {
                int mid = left + (right - left) / 2;
  
                if (nums[mid - 1] > nums[mid]) {
                    return mid;
                } else if (nums[mid] > nums[left]) {
                    left = mid;
                } else {
                    right = mid;
                }
            }
  
            return nums[left] > nums[0] ? 0 : left;
        }
  
        private int binarySearch(int[] nums, int startIdx, int endIdx, int target) {
            int left = startIdx;
            int right = endIdx;
  
            while (left + 1 < right) {
                int mid = left + (right - left) / 2;
  
                if (nums[mid] == target) {
                    return mid;
                } else if (nums[mid] < target) {
                    left = mid;
                } else {
                    right = mid;
                }
            }
  
            if (nums[left] == target) {
                return left;
            }
  
            if (right < nums.length - 1 && nums[right] == target) {
                return right;
            }
  
            return -1;
        }
    }
  

The complexity of Binary Search is:

• Time complexity: O(log(n)).
• Space complexity: O(1).

Wrapping up

• Understanding why we can apply Binary Search in this problem.

• Go from the brute-force solution, then optimize it.