Table of contents


Given problem

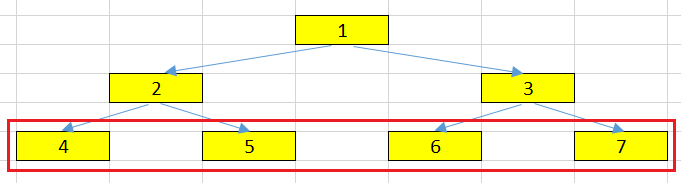
Given a tree that looks like an below image.

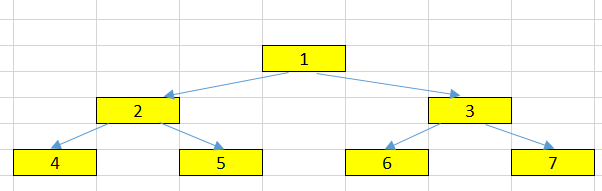
In this article, we will understand some common concepts such as:

  • Node and some things around it.
  • Degree
  • Edge
  • Path
  • Distance
  • Depth
  • Level
  • Height
  • Width


Node of a Tree

A node is a structure which may contain a value or condition, or represent a separate data structure.

In an above image, we can have some nodes:

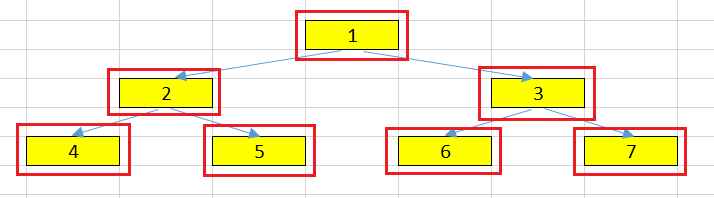
Normally, in binary tree, we can define a node like that.

class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;
}

Belows are some concepts that are relevants to a Node.

  1. Root node

    The top node in a tree, the prime ancestor.

    For example, our root node in an above tree is 1.

  2. Child node

    A node directly connected to another node when moving away from the root, an immediate descendant.

    For example, 2 and 3 are the child nodes of the root node - 1.

  3. Parent node

    The converse notion of a child, an immediate ancestor.

    For example, 1 is the parent node of two child nodes: 2 and 3.

  4. Sibling nodes

    A group of nodes with the same parent.

    For example, 2 and 3 are the sibling nodes. They have the same parent node - 1.

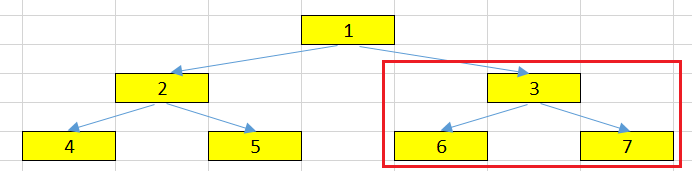
  5. Descendant node

    A node reachable by repeated proceeding from parent to child. Also known as subchild.

    For example, 3, 7, and 6 are descendant nodes of 1.

  6. Ancestor node

    A node u is an ancestor of a node v if v is contained in the subtree rooted at u; we may write equivalently that v is a descendant of u.

    For example, 1 is an ancestor node for every node such as 2, 3, 4, 5, 6, and 7.

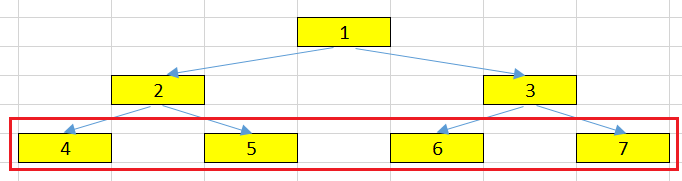
  7. Leaf node

    A node with no children.

    For example, 4, 5, 6 and 7 are leaf nodes in our tree.


Degree of a Node

For a given node, it’s the number of children. A leaf is necessarily degree zero.

The degree of a tree is the maximum degree of a node.

For example:

  • the degree of node 1 is 2 because it has two nodes: 2 and 3.
  • the degree of an above tree is 2.


Edge, Path, and Distance

  1. Edge

    Edge is the connection between one node and another.

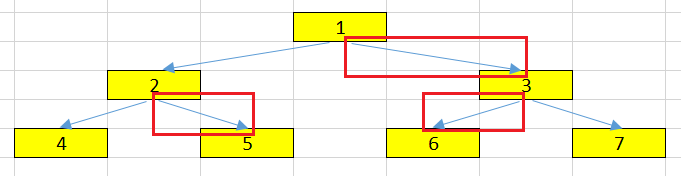
  2. Path

    Path is a sequence of nodes and edges connecting a node with a descendant.

    Path includes all nodes and all edges along the path, not just edges.

    For example, the path between two nodes 4 and 5 is: 4 –> 2 –> 5.

  3. Distance

    The number of edges along the shortest path between two nodes.

    For example, the distance between 4 and 5 is 2.


Depth, Level, Height, and Width

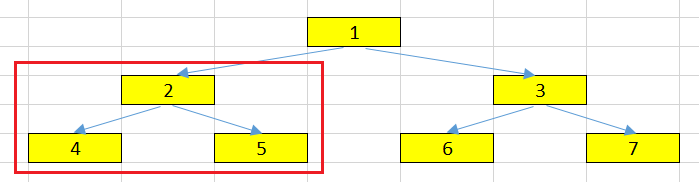
  1. Depth

    The distance between a node and the root.

    The depth of the root node is 0.

    For example, the depth of 5 node is 2.

  2. Level

    The level of a node is defined by 1 + the number of edges between the node and the root.

    Below is the relationship between Level and Depth concepts.

     Level = Depth + 1

    The level of root node is 1.

    For example, the level of 6 node in an above tree is 3.

    Below is the source code that calculates the maximum level of binary tree.

    We use top-down recursive version for this problem because:

    • the starting point is the root node.
    • we know that the level of root node is 1.
     public class MaxLevelTree {

     private static int maxHeight = Integer.MIN_VALUE;

     private static void getMaxLevelTopDown(TreeNode root, int level) {
         if (root == null) {
             return;
         }

         if (root.left == null && root.right == null) {
             maxHeight = Math.max(maxHeight, level);
         }

         getMaxLevelTopDown(root.left, level + 1);
         getMaxLevelTopDown(root.right, level + 1);
     }
 }

  3. Height

    The height of a node is the number of edges on the longest downward path between that node and a leaf.

    For example:

    • the height of root node is 2.
    • the height of 2 node is 1.

    Below is the source code to calculate the height of binary tree. We will use bottom-up recursive version because:

    • if the node is null, then its height is -1.
    • the leaf node’s height is 0.
    • It means that we have sufficient information about the height of the children nodes.
     public static int getHeightTree(TreeNode root) {
     if (root == null) {
         return -1;
     }

     int leftHeight = getMaxLevelBottomUp(root.left);
     int rightHeight = getMaxLevelBottomUp(root.right);

     return Math.max(leftHeight, rightHeight) + 1;
 }

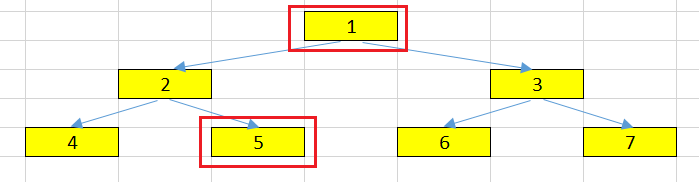
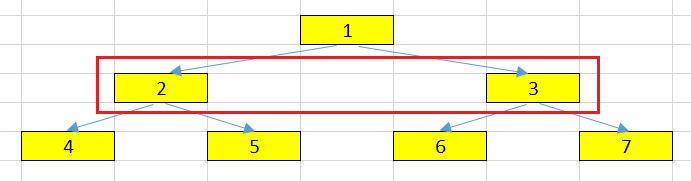
  4. Width

    The number of nodes in a level.

    For example:

    • at the level = 2, we have two nodes such as 2 and 3.

    • at the level = 3, we have four nodes.


Wrapping up

  • With depth and level concept, remember that it compares with the root node.

  • With height concept, it compares with the leaf node.

Refer:

https://en.wikipedia.org/wiki/Tree_%28data_structure%29

https://www.cs.yale.edu/homes/aspnes/pinewiki/BinaryTrees.html?highlight=%28CategoryAlgorithmNotes%29