Table of contents
Given problem
Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.
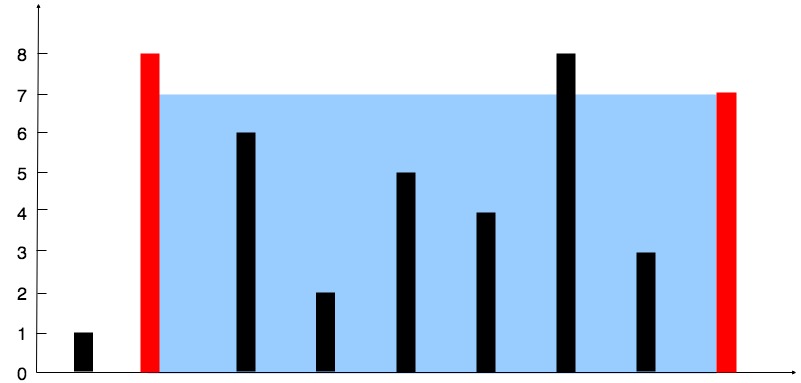
For example:
- Input: [1,8,6,2,5,4,8,3,7]
- Output: 49
Using brute force solution
In order to solve this problem by using brute force solution, we will use two loops.
- In outer loop, use
iindex to iterate elements from0tolength - 1. - In inner loop, use
jindex to iterate elements fromlength - 1to0. - The termination conditions is
i = j.
public static int maxArea(int[] height) {
int len = height.length;
int maxWater = Integer.MIN_VALUE;
for (int i = 0; i < len; ++i) {
for (int j = len - 1; j > i; --j) {
int minHeight = Math.min(height[i], height[j]);
maxWater = Math.max(maxWater, minHeight * (j - i));
}
}
return maxWater;
}
The complexity of the brute force solution:
- Time complexity: O(n^2).
- Space complexity: O(1)
Using two pointers technique
From the brute force solution, we can find that we are using two loops with two indexes to loop all elements. These indexes will scan all cases but it can cause redundancy.
For example, with input = [1,8,6,2,5,4,8,3,7], we have:
-
In the first time of outer loop, we will calculate all cases from (0, length - 1), (0, length - 2), …, (0, 1).
In this loop, we only need the case (0, length - 1). Because we need to keep the size of (j - i) is maximum, with j is the index of inner loop, i is the index of outer loop; and the necessary height’s value is equal to the min of (height[i], height[j]).
-
Continue with the above same thing, we can use the two pointers technique.
public static int maxArea(int[] height) {
int left = 0;
int right = height.length - 1;
int maxArea = Integer.MIN_VALUE;
while (left < right) {
maxArea = Math.max(maxArea, Math.min(height[left], height[right]) * (right - left));
if (height[left] < height[right]) {
++left;
} else {
--right;
}
}
return maxArea;
}
The complexity of the two pointers technique:
- Time complexity: O(n)
- Space complexity: O(1)
Wrapping up
- Understanding about how to use two pointers technique.
Refer: