Quick Union

In this tutorial, we will discuss about Quick - Union to understand all of it. Then, we can know about which problem will be applied Quick-Union.

Introduction to Quick Union
Source code
Drawbacks of Quick Union
Application of Union-Find
Wrapping up

Introduction to Quick Union

A disjoint-set is a data structure that keeps track of a set of elements partitioned into a number of disjoint (non-overlapping) subsets. A Union-Find algorithm is an algorithm that performs two useful operations on such a data structure:

Find: Determine which subset a particular elements is in. This can be used for determining if two elements are in the same subset.
Union: Join two subsets into a single subset.

And Quick Union is one of the implementations of Union-Find algorithm. And it’s an algorithm for solving the dynamic connectivity problem, also called lazy approach.

Some implementations of Union-Find algorithm:

Quick Find
Quick Union
Weighted quick union
Weighted quick union with path compression

Source code

Data structure
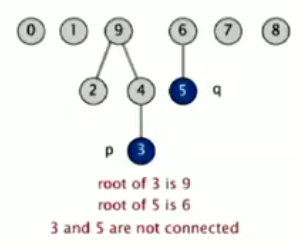
- Maintain integer array id[] of size N.
- Interpretation: id[i] is parent of i.
- Root of i is: id[id[id[…id[i]…]]]
Find operation: check if p and q have the same root.
Union operation: to merge components containing p and q, change all entries whose id equals id[p] and id[q]. So, we have a problem: many values can be changed.
Analysis:
- Find operation takes time proportional to depth of p and q in tree.
  - could be proportional to N.
- Union operation takes constant time, given roots.

public class QuickUnionUF {
    
    private int[] id; 
       
    // set id for each object to itself 
    // (N array accesses)
    public QuickUnionUF(int N) {
        id = new int[N];
        for (int i = 0; i < N; ++i) {
            id[i] = i;
        }
    }
       
    // chase parent pointers until reach root 
    // (depth of i array accesses)
    private int root(int i) {   // find operation
        while (i != id[i]) {
            i = id[i];
        }
        
        return i;
    }
    
    // check if p and q have same root
    // (depth of p and q array accesses)
    public boolean connected(int p, int q) {
        return root(p) == root(q);
    }
    
    // change root of p to point to root of q (depth of p and q array acceses)
    public void union(int p, int q) {
        int i = root(p);
        int j = root(q);
        
        id[i] = j;
    }
}

Drawbacks of Quick Union

Cost model: number of array access (for read and write)

algorithm	initialize	union	find
quick-find	N	N	1
quick-union	N	N (*)	N (worst case)

* : includes cost of finding roots.

Quick-find defect
- Union too expensive (N array accesses)
- Trees are flat, but too expensive to keep them flat
Quick-union defect
- Trees can get tall
- Find operation is too expensive (could be N array accesses)
So, we could wind up with a long skinny tree. Of each object just pointing to next and then to do a find operation for object at the bottom would involve going all the way through the tree.

Costing involving in the array accesses is just to do the find operation and that’s going to be slow if we have a lot of operations.

Finally, the maximum number of array accesses during a find operation when using the quick-union on n elements is linear.

Quick-Union Improvements

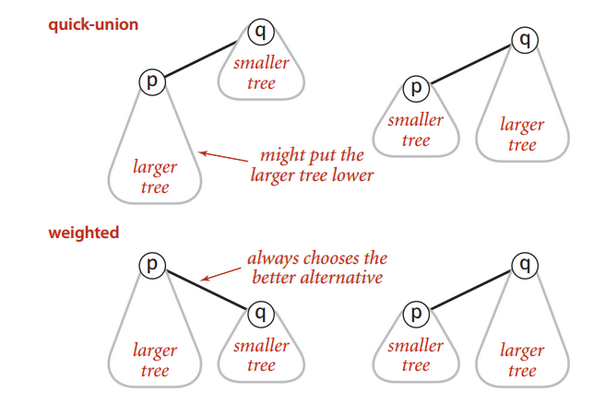
Weighted quick-union

How to improve:
- Modify quick-union to avoid tall trees.
- Keep track of size of each tree (number of object)
- Balance by linking root of smaller tree to root of larger tree (reasonable alternatives: union by height or rank).

Source code

Data structure: same as quick-union, but maintain extra array sz[i] to count number of objects in the tree rooted at i.
Find operation:
- Identical to quick-union.
- Takes time proportional to depth of p and q.
```
  return root(p) == root(q);
```

Union operation: Modify quick-union to:

Link root of smaller tree to root of larger tree.
Update the sz[] array.

Takes constant time, given roots.

  int i = root(p);
  int j = root(q);

  if (i == j) return;

  if (sz[i] < sz[j]) {
      id[i] = j;
      sz[j] += sz[i];
  } else {
      id[j] = i;
      sz[i] += sz[j];
  }

Proposition: Depth of any node x is at most lgN.

lg = base-2 logarithm.

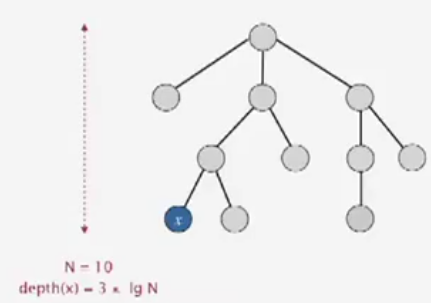
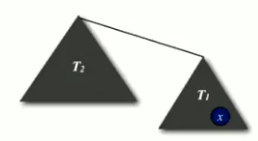
algorithm	initialize	union	connected
quick-find	N	N	1
quick-union	N	N *	N
weighted QU	N	lgN *	lgN

*: includes cost of finding roots.

Pf. When does depth of x increase?

Increases by 1 when tree T1 containing x is merged into another tree T2.

The size of the tree containing x at least doubles since

Size of tree containing x can double at most lgN times.

Q: Stop at guaranteed acceptable performance? A: No, easy to improve further.

Analysis:
- Modify quick-union to avoid tall trees.
- Keep track of size of each component.
- Balance by linking small tree below large tree.
- Time taken for union and connected commands is at most the depth of the tallest tree, which is O(logN) at most.
  
  Proof: When T1 is merged to T2, where T1 <= T2, the depth of T1 will increase by 1. Now, the depth of T2 (after merging) will increase by 1 if merged with T3, where T3 >= T2. So, every time, we need a tree X >= tree Y, to increase the depth of tree Y by 1. Therefore, the size of T1 can increase at most logN.
Find operation:
- The weighted quick-union algorithms will link the root of the smaller of the two trees to the root of the larger of the two trees.
- The distance from each node to the root of its tree is small, so the find operation is efficient.
Union operation:
- The worst scenario for weighted quick-union algorithm is that each union operation links trees of equal size. If the number of objects is less than 2^n, the distance from any node to the root of its tree is less than n.
Some question for weighted quick-union
- Is performance improved?
  - Theory: lgN per union or find operation.
  - Practice: constant time.
- Example: huge practical problem.
  - 10^10 edges connecting 10^9 nodes.
  - reduces time from 3000 years to 1 minute.
  - Supercomputer wouldn’t help much.
  - Good algorithm makes solution possible.
- Stop at guaranteed acceptable performance?
  - Not hard to improve algorithm further.

Path compression

Quick union with path compression: Just after computing the root of p, set the id of each examined node to point to that root.
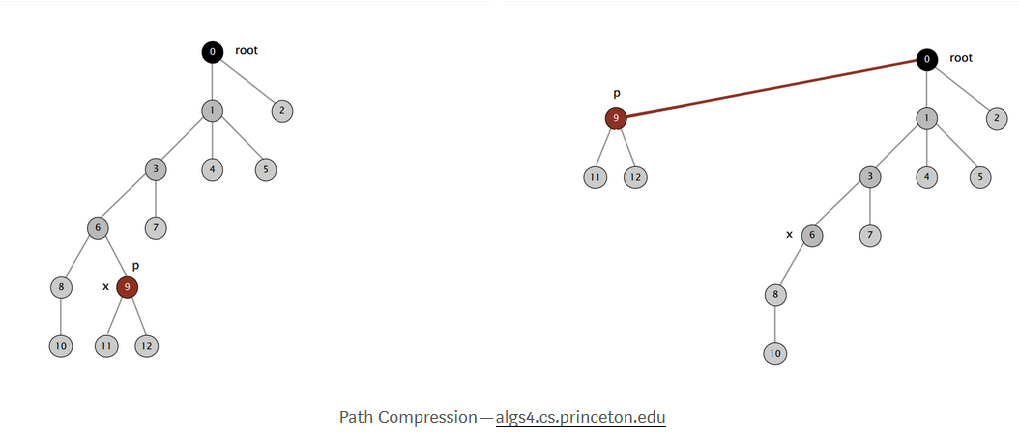
- Two-pass implementation: add second loop to root() to set the id[] of each examined node to the root.
- Simpler one-pass variant: Make every other node in path point to its grandparent (thereby halving path length).
```
  private int root(int i) {
      while (i != id[i]) {
          id[i] = id[id[i]];
          i = id[i];
      }

      return i;
  }
```
Note: In pratice, no reason not to! Keep tree almost completely flat.

Weighted quick-union with path compression

Theorem: A sequence of M union and find operations takes O(N + M lg* N) time.

Informally it provides an upper bound on the running time.
lg* is the iterate logarithm function. It refers to the number of times that the logarithm function must be iterated until the resulting number is less than 1. This function grows very slowly.
lg* N grows so slowly that we may as well consider it to be a constant.
So the algorithm is linear. The running time is constant factor of the time it takes to read in the data.
So the algorithm could be used in online mode, solving the problem at the same rate that data is read in.

It’s nice when an algorithm has this property, since data can be processed in real time. Unfortunately parsing algorithms for context free languages normally run in cubic time, so real time natural language processing is not possible. Or at least one can say that real time natural language processing is not possible under the assumption that context free parsing is necessary. Perhaps more superficial chunk parsing suffices.

N	lg*N
1	0
2	1
4	2
16	3
65536	4
2^65536	5

Iterate log function

Linear-time algorithm for M union-find ops on N objects?

Cost within constant factor of reading in the data.
In theory, Weight Quick-Union with Path Compression is not quite linear.
In practice, Weight Quick-Union with Path Compression is linear.

Summary

Bottom line: Weighted quick union (with path compression) makes it possible to solve problems that could not otherwise be addressed.

algorithm	worst-case time
quick-find	M N
quick-union	M N
weighted Quick-Union	N + MlogN
QU + path compression	N + MlogN
weighted QU + path compression	N + Mlg*N

M union-find operations on a set of N objects.

For example:

10^9 unions and finds with 10^9 objects

WQUPC reduces time from 30 years to 6 seconds.
Super computer won’t help much.
Good algorithm enables solution.

Application of Union-Find

Percolation
Games (Go, Hex)
Dynamic connectivity
Least common accessor
Equivalence of finite state automata
Hoshen-Kopelman algorithm in physics
Hinley-Milner polymorphic type inference
Kruskal’s minimum spanning tree algorithm
Compiling equivalence statements in Fortran
Morphological attribute openings and closings
Matlab’s bwlabel() in image processing

Wrapping up

When opening one new site in the percolation simulation, how many times is union() called?

–> Solution: 0, 1, 2, 3 or 4. It is called for each neighboring site that is already open. There are 4 possible neighbors, but some of them may not already be open.
Social network connectivity.

Given a social network containing nnn members and a log file containing m timestamps at which times pairs of members formed friendships, design an algorithm to determine the earliest time at which all members are connected (i.e., every member is a friend of a friend of a friend … of a friend). Assume that the log file is sorted by timestamp and that friendship is an equivalence relation. The running time of your algorithm should be mlog⁡n or better and use extra space proportional to n.
Union-find with specific canonical element.

Add a method find() to the union-find data type so that find(i) returns the largest element in the connected component containing iii. The operations, union(), connected(), and find() should all take logarithmic time or better.

For example, if one of the connected components is {1,2,6,9}, then the find() method should return 999 for each of the four elements in the connected components.
Successor with delete.

Given a set of nnn integers S={0,1,…,n−1} and a sequence of requests of the following form:
- Remove xxx from SSS
- Find the successor of x: the smallest y in SSS such that y ≥ x.
design a data type so that all operations (except construction) take logarithmic time or better in the worst case.